Overview
The Perpetual Protocol (PERP) is an early stage decentralized derivatives platform that mimics centralized derivatives products found on the likes of Bitmex, FTX and Deribit. Many of the fundamental concepts remain the same but the primary difference is how price discovery is established. Centralized exchanges utilize a central limit order book (CLOB) where market makers provide liquidity at various price levels, and traders consume said liquidity in these order books to establish positions. Supply and demand forces between buyers (longs) and sellers (shorts) determine the directional trend. In contrast, Perpetual Protocol utilizes an innovative price discovery mechanism, a virtual Automated Market Maker (vAMM), that leans on the concept of AMMs where capital is pooled together and tendered by a deterministic algorithm, rather than individual providers. However, since the derivative instrument is synthetic and no real assets are directly exchanged, the vAMM is able to maintain the feature of price discovery via an algorithm while removing the undesirable quality of impermanent loss that liquidity providers suffer when allocating capital into a pool and subsequently being traded against.
AMM Backdrop
In AMMs, allocators (called LP’s) aggregate equal weights of capital pairs into pools. These capital pools agree to provide liquidity algorithmically, based on some predefined deterministic formula. Contrast this to the job of market makers on centralized exchanges, who provide liquidity based on their independent utility preference and proprietary, dynamic formulas. In this way, AMMs automate away the role of market makers, allowing any individual to allocate capital to the pool, and “set it and forget it” to earn passive commission fees. While AMMs induce their own set of challenges, the primary advantages for traders is the ability to determine the exact cost of a position prior to execution (since the pricing formula is a constant mathematical equation), as well as knowing that the system will always quote you liquidity (desirable for interoperability).
Perpetual Swaps Backdrop
Perpetual swaps are a set of derivative instruments that provide synthetic price exposure to an asset without having to own the underlying. Pioneered by Bitmex’s XBTUSD, perpetual swaps have proliferated in the crypto community for a variety of reasons:
Leverage: Unlike margin trading, where someone is physically loaning you USD to buy assets in the spot market, leverage is synthetically spawned by traders borrowing against their own collateral.
Liquidity: Aggregate liquidity in the derivatives market is considerably higher than the spot markets, creating tighter spreads.
Cost: Owning price exposure means traders don’t have to worry about carry cost (i.e. cost to secure/custody the underlying asset).
Composite Indexes
Perpetual contracts have an underlying index in which the derivative is designed to track. Composite indexes are the ‘derive’ component of ‘derivative’. This index can vary in structure: it could be as simple as an API feed from a single centralized exchange, or it could be a time-weighted-average-price of various centralized exchange API feeds bundled together.
Bitmex’s Perpetual contract, XBTUSD, has a reference index price of 5 BTC/USD spot exchange API’s: Kraken, Gemini, Bitstamp, Coinbase Pro and Bittrex. Each API has a different weighting in the Composite Index. The goal is to make the composite index redundant to outlier movements or manipulation stemming from a single feed.
Going forward, we will refer to XBTUSD as the derivative instrument, and BTCUSD as the composite index.
While the objective of XBTUSD contract is to mimic the behavior of BTCUSD as tightly as possible, ultimately there will never be perfect union of the two prices, unless there is perfect supply/demand equilibrium between the spot and derivative orderbooks: an impossible assumption. What happens if the buy pressure on Bitmex explodes, but remains relatively constant on the spot? In such a scenario, the price of the XBTUSD contract would increase, while the BTCUSD index would remain flat. The derivative has deviated from the underlying oracle.
To overcome this situation, Bitmex introduces an incentive mechanism called “funding rate” which naturally aligns the peg. Funding is a reoccurring 8-hour interest payment, paid by the contract side where the premium exists.
If funding is positive (i.e. derivative price > spot price) then longs will pay shorts the premium. If funding is negative (i.e. derivative price < spot price) then shorts will pay longs the premium.
Example : Suppose the price of spot index is $50,000/BTC, while the derivative trades at $55,000/BTC. In this scenario, funding is positive (derivative price > spot price). Thus, XBTUSD longs would pay an interest rate to maintain their position, with the proceeds accruing to their counterparties that are short XBTUSD. Longs are paying for counterparty liquidity. This relationship would exhibit in the opposite direction if there were more short demand than long demand; shorts would pay longs.
The greater the differential between the derivative and spot prices, the higher the interest payment. As that interest rate floats higher, it incentivizes more counterparty liquidity to step in and take the opposite side of the trade to collect that fee.
But what happens if the price of bitcoin is rapidly appreciating? Sure, you are set to make a marginal interest payment every 8h, but what if the loss of principle on the short is drastically outpacing your accrued funding payment?
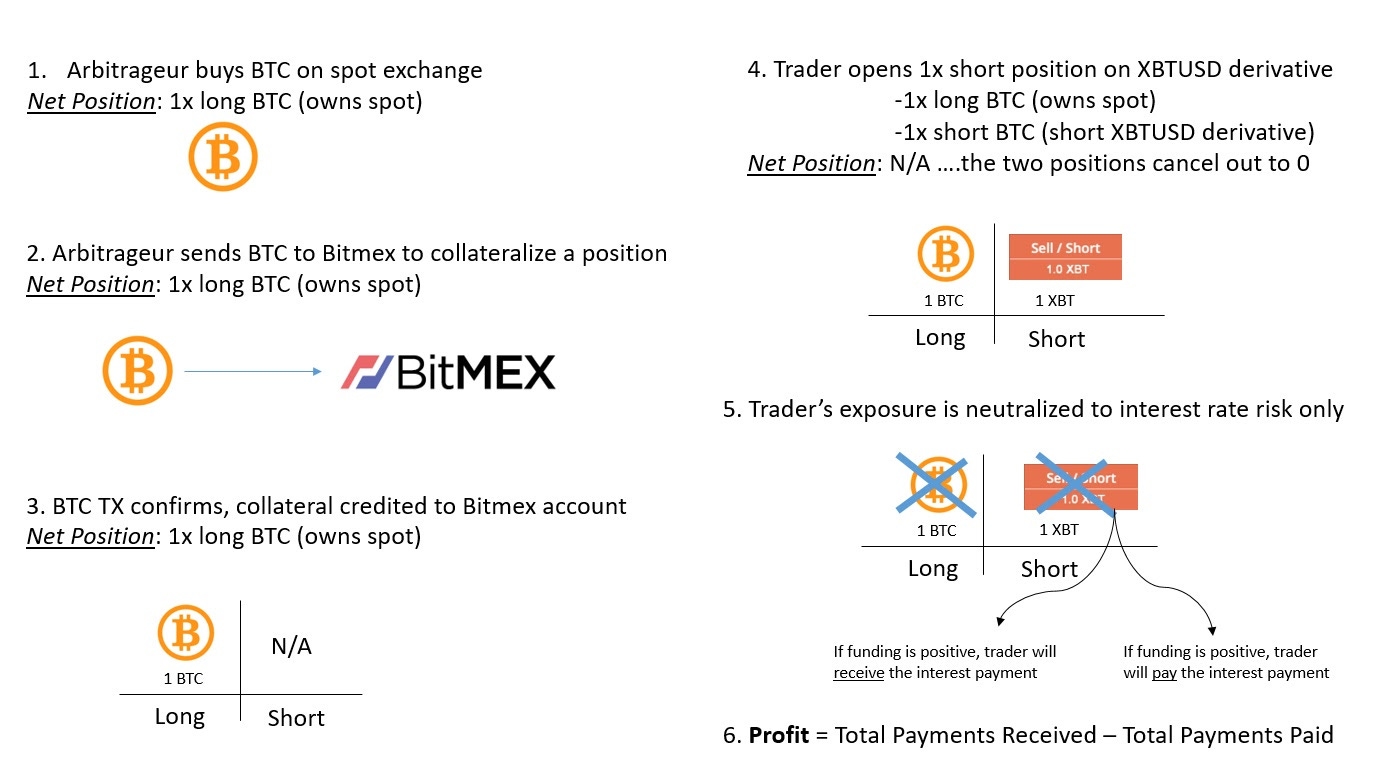
Enter Arbitrage
An interesting arbitrage opportunity exists where traders can hedge away directional risk, isolating the interest payment from funding. Here’s how it works:
Suppose the trader bought $100,000 of BTC and then opened up a 1x short position with it. To calculate how much interest he would earn/pay, we would simply multiply the interest rate * the notional size of the trader’s position. Assuming the “default” funding rate of 0.01%, over the 8h window the trader would receive:
$100,000 * 0.01% = $10
This might not seem like a lot at first, but what if we annualize this value?
$10 * 3 = $30/day
$30 * 365 = $10,950/ year
$10,950/ $100,000 = 10.95% for a directional risk-free trade
0.01% is the baseline default rate, however many times funding payments can be much higher. Historically, this trade has annualized out in the range of 20-30% APR. During a bull run, it can be much higher, as demand for leverage skyrockets, and participants are willing to pay a large premium for that counterparty liquidity.
Perpetual Protocol
Perpetual Protocol is similar to Bitmex, in the sense that it is a 0-sum derivatives marketplace, where the derivative and spot markets operate independently of one another. Price discovery happens natively on both platforms, but when the demand is higher on the derivative market than the spot, a funding rate is charged to longs as an incentive to bring the peg back in line (and vice versa). The disequilibrium creates an opportunity for market neutral actors to step in and capture a risk free arbitrage, and in doing so, make price discovery more efficient.
The primary difference between Bitmex and Perpetual Protocol is that the price on Bitmex is established via a traditional order book method, while on Perpetual, price is established based on an AMM algorithmic variant called a vAMM. Before diving into the vAMM let’s recap the basics of how price discovery works in a CLOB.
In the CLOB model, Market makers have total and indiscriminate control over 1) at what price point they are willing to offer liquidity 2) how much liquidity they are willing to extend at said price points. Each market maker has differentiating cost of capital, liquidity, risk profile, utility function etc. This range of variety is what keeps market liquidity a dynamic and ever changing variable.
The role of market makers boils down to a simple axiom: with each successive order hitting the books, differentiate between informed and uninformed order flow. Provide liquidity to the uninformed, and avoid (or charge premium) to the informed. Market makers must observe not only various market forces, but the actions of other market makers in the ecosystem. Action by a peer may be indicative of superior information they may not be aware of. The culmination of these forces creates a dynamic relationship of liquidity, where, as volatility skyrockets it tends to disappear (when it ironically is most needed). This ability to turn liquidity on and off is good for market makers, as it protects their backend, but detrimental for traders.
AMMs transform this liquidity relationship from dynamic to static. It does this by removing all the individual actors with independent pricing functions, replacing them with a deterministic formula that offers quotes based on how much of the two assets exists in the pool, and how much liquidity the current order is attempting to consume. This is fantastic for traders because they have guaranteed certainty of liquidity, and absolute certainty of cost of execution on a taker order (cannot be guaranteed in a CLOB model). It comes at the expense of the Liquidity Providers (LP’s); the individuals providing liquidity into the pools, where that liquidity is then provisioned by the algorithm as an “automated market maker”. This happens because the algorithm is bound to offer liquidity based on a very primitive mathematical equation, even if it is economically damaging to do so. The algorithm lacks the “market knowledge” to know when to shut off, or adjust its pricing model. This leads to the problem of impermanent loss.
Impermanent Loss
AMM exchanges are disconnected from the "reality" of external markets. This is because there are no market makers who can dynamically update their offers in order to respond to unique situations happening in the market. Instead, an AMM marketplace replaces these independent actors with a generalized, deterministic algorithm (x*y=k) as the sole methodology for issuing price quotes. But just because an AMM algorithm can issue a price quote, does not mean its quote is competitive.
For example, the ETH/USDC pair might be at 110 on Coinbase, Binance, Gemini etc, but trades at 100 on Uniswap. Unfortunately, because this quote is mathematically derived from how much capital sits inside the liquidity pools, there is no possible way that the x*y=k formula can alter its native pricing structure to produce a more competitive quote that matches it CEX competitors. The only way that the price on uniswap can match that of the CEX is if the underlying liquidity pool itself changes. And for the liquidity pool to change, external actors need to change the composition of the pool by depositing/removing assets from it.
Here in lies the dilemma of AMM’s that manifests itself the form of impermanent loss: Suppose the SEC announces approval of an ETH ETF and ETH/USDC immediately skyrockets 20% on Coinbase from $100 to $120. seeing the explosion of buy side demand, CEX market makers will pull their existing offers at $100, and revise their orders by raising ask prices until equilibrium in the market is established. In contrast, an AMM cannot dynamically respond to such forces. It will continue to offer quotes ~$100 until the material composition of the underlying pool is altered. This creates an arbitrage opportunity, and this arbitrage ultimately allows price on the AMM to re-converge towards the broader market equilibrium.
Arbitrage Example
Following up from the last example, if ETH is selling for $100 on Uni, an arbitrage agent will buy that “cheap” ETH by depositing 100 USDC into the pool and removing 1 ETH. They’ll then take that 1 ETH and sell it on the CEX for $120 and pocket the difference. With each successive iteration of this arbitrage, the pool is revoking more of its ETH and marginally replacing it with more USDC. This pushes the price of the ETH/USDC pair upwards, until it is in line with the $120 price quote exhibited on the CEX. With the DEX and CEX prices re-converged, arbitrage agents have no profit left to extract, and will complete their interactions with the protocol.
We must ask the question: if arbitrageurs are extracting profit from the protocol by buying these “discount” assets and flipping them on the CEX, who ultimately bears the cost of this interaction? The answer is Liquidity Providers in the pool. In the scenario above, the algorithm is selling off their quality ETH at a price well below the prevailing market rate. Unfortunately, because the liquidity provisioning process is governed by this strict x*y=k formula, there is no manner in which they can prevent this situation from occurring, outside of leaving the pool altogether.
Impermanent loss is not all evil (or at minimum a necessarily evil), because it provides the AMM system with a native price discovery mechanism that ultimately allows the AMM quote to reconvene with the external market rate, without having to rely on an oracle module. Arbitrageurs are providing a valuable service to the network and need to be compensated for the services they provide. The challenge lies in finding an equilibrium compensation point where the Liquidity Providers aren’t overpaying for this performed service. This is why we are seeing AMMs reformulating their formulas, or offering LPs to define certain parameters in which they will provide liquidity, in order to cut down the impermanent loss to a more sustainable metric.
vAMM
Virtual AMMs (vAMMs) are a novel concept of applying a price discovery mechanism to derivatives, without relying on an orderbook.
As a derivative, the Perpetual Protocol does not actually exchange any assets. All it does is replicate price exposure to certain assets. Contracts are collateralized and PnL settled in USDC.
Because there is no actual asset swap, there is no need for liquidity providers to post collateral into a pool. Similar to other derivative platforms, traders bring collateral to the pool in the form of USDC, and then open positions against that margin collateral, essentially borrowing against their own equity. Leverage parameters are established by the exchange (currently 10x on Perpetual Protocol), and with that, a specified level of collateral equity that must be maintained. Failure to maintain the required level will result in a forced closure of the position by the protocol, and a seizure of collateral.
In the CLOB derivative model, a direct counterparty is involved for each contract in existence, meaning for each long position in the system, there is a short matched with it. So, the total number of longs will always equal the total number of shorts. The counterparty’s margin collateral is where profit accrues from: if the price is going up, the long position is winning, and the short position is losing by a linear amount. The long’s profits accumulate directly from the short’s losses. The rest of the mechanics stay the same. Price of the derivative moves by takers consuming maker’s liquidity. When the demand for long contracts > short contracts, price of the derivative goes up, and vice versa.
A vAMM model looks considerably different. A vAMM does not require direct counterparty matching (i.e. pairing of a long and a short). Gains are extracted from the incremental price paid by each marginal buyer (quoted by the x*y=k algorithm). This has drastically different implications; primarily that you no longer need an equal value of long and short contracts. In theory, everyone trading on the platform could be long, and the system would be perfectly functional.
Next, we will explore the dynamics of the algorithm, and how it arrives at the price quote that is issued to traders who come to the exchange looking to take on a position. In addition, we will demonstrate how profit accrues and settles within the system.
vAMM Quote Example
PERP DAO configures the initial parameters of x,y,k in the vAMM
Alice longs ETH on 200 USDC. How much ETH will the vAMM quote her? First, compute the new x value of the pool, given the change in y
x* 10,200 = 1,000,000
x = 98.039 ETH
Alice's Delivery = Old x - New x
(100-98.039) = 1.961 ETH
Alice gets 1.961 ETH for her 200 USDC…Exchange rate = 101.99USDC/ETHAfter seeing Alice get long, Bob too decides to get long with 200USDC. How much will the vAMM quote him?
-First, compute the new x value of the pool, given the change in y
x* 10,400 = 1,000,000
x = 96.154 ETH
Bob's Delivery = Old x - New x
(98.039-96.154) = 1.885 ETH
Bob gets 1.885 ETH for his 200 USDC…Exchange rate = 106.10USDC/ETHAlice then decides to close out her 1.961 ETH long. How much USDC will the vAMM quote her?
First, compute the new y value, given change in x
* Note: this calculation reverses the variable we are solving for, since Alice is giving back her ETH in exchange for USDC
98.115* y = 1,000,000
y = $10,192.12 USDC
Alice's Delivery = Old y - New y
(10,400 - 10,192.12) = 207.88
Alice gets 207.88 USDC for her 1.961 ETH…but only paid 200 USDC at onsetNet profit = (207.88 - 200)
7.88 USDCSeeing Alice close her long Bob decides to close his long. How much USDC will the vAMM quote him?
First, compute the new y value, given the change in x
100* y = 1,000,000
y = $10,000 USDC
Bob's Delivery = Old y - New y
(10,192.12- 10,000) = 192.12
Bob gets 192.12 USDC for his 1.885 ETH…but paid 200 USDC at onsetNet profit = (192.12 - 200)
- 7.88 USDC
Summary of the primary differences between AMM and vAMM:
With the AMM, a group of individuals actually delivered 100 ETH and 20,000 USDC into the pool. A physical allocation occurred. With the vAMM, there are no LP’s posting collateral that will subsequently be traded against. Instead, the creator of the derivative contract artificially configures the value of x and y according to their choosing. If the market rate is 200USDC/ETH, they could set the parameters to:
100 ETH and 20,000 USDC
150 ETH and 30,000 USDC
500 ETH and 100,000 USDC
10,000 ETH and 2,000,000 USDC
As we will touch on later in the post, raising/lowering the total values of x and y will have tradeoffs in both positive and negative directions. But we can configure the initial parameters in any manner we desire, so long as they are in fixed denominations.
Remember the arbitrage opportunity that exists in the AMM example, where a user could buy ETH on Coinbase for $200 and sell it for $202 on Uniswap? That opportunity doesn’t exist in Perpetual Protocol, because there are no liquidity providers posting assets into a pool, and no provisioning of these assets via swaps. A trader cannot withdraw vETH or vUSDC and sell it on coinbase, as it is an unrecognized synthetic asset. Thus there is no impermanent loss. However, without impermanent loss, we are left with the problem of dislocated pricing between the spot market and the derivative market. Therefore, we introduce a funding rate to tether the two instruments back in line.
Liquidation Mechanics
The maintenance margin is 6.25%. If a trader’s margin ratio falls below this amount, they are subject to a process called liquidation, where the system seizes the position and forcefully closes it out, taking the trader’s collateral with it. So, if a trader’s position moves against them and starts approaching the maintenance margin, they will want to a) deposit more collateral to “refill” their margin ratio b) trim down their position size so that continued downtrend does not wipe them out. On sites like Bitmex the moment the maintenance margin is breached the exchange liquidation engine automatically seizes the collateral and unwinds the position into the market. With Perpetual Protocol however this isn’t possible. Smart contracts and blockchains in general are passive and cannot execute code without external triggers. So the system utilizes “keeper” bots that anyone can program and run. These keepers continually scan the blockchain looking for liquidation conditions, and if such conditions are met, the keeper triggers the liquidation protocol. As a reward, they get to pocket a % of that trader’s margin balance.
PERP token
The Perpetual Protocol has its own native utility token, PERP, that serves as an equity-style value accrual mechanism to the protocol. PERP holders receive 50% of all trading commissions generated by the system (remaining 50% goes to the insurance fund). In addition to being a utility token, PERP also substitutes as a governance token, giving holders a voice in protocol voting. We can think of PERP stakers as a value accrual replacement for equity owners in Bitmex, as well as governors of the platform setting what type of assets are available to trade.
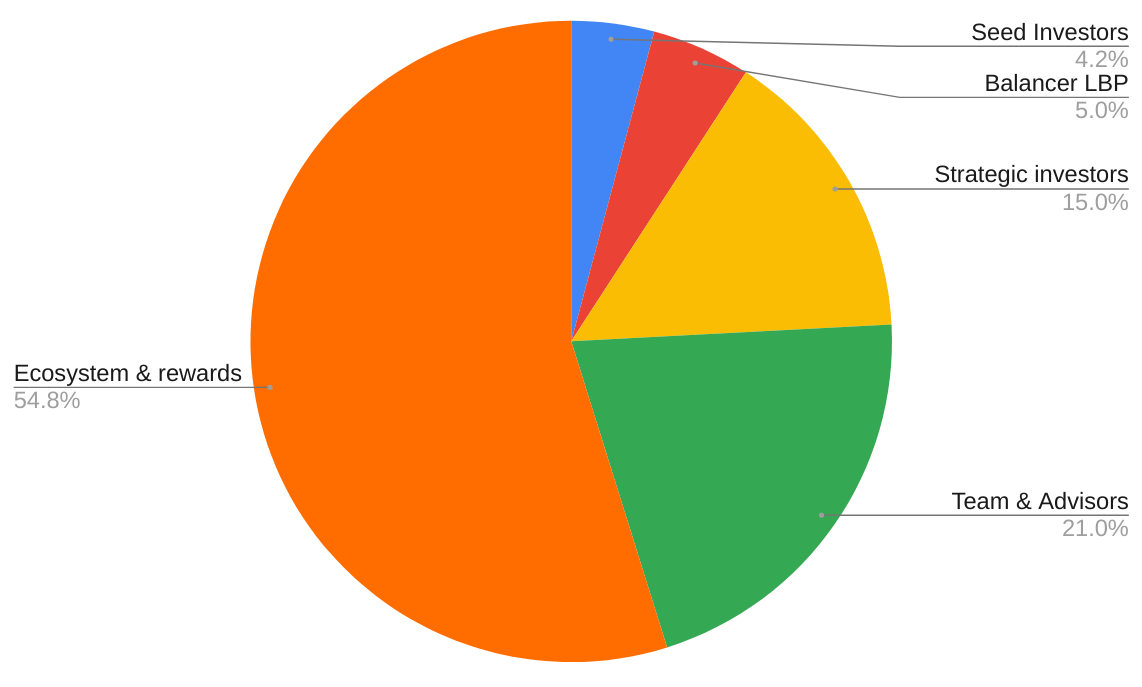
PERP has a semi-hard supply cap at 150,000,000. Coins were premined at inception and distributed according to the following parameters:
Associated Lockups:
Seed Investors – 25% unlocked at mainnet launch, 25% every 3-months afterward
Strategic Investors - Same as seed
Balancer Liquidity Bootstrapping Pool - No lockups
Team and Advisors - tokens unlock 6 months after mainnet launch at a rate of 2.1% every 3-month period
Ecosystem and Rewards - No unlock period, but funds must go through governance approval before being used
PERP so far has engaged in 2 liquidity incentivisation programs in its short history; Balancer LBP program and its Transaction Mining Program.
Transaction mining was a program to bootstrap liquidity that involved rebating trader’s commission fees, depending on how long they held the position open. We can conceptualize this model similar to the way that exchanges offer a maker rebate to makers (in exchange of performing a valuable service to the platform of providing liquidity). If a Perpetual Protocol trader held a position for more than 30m on the platform, they were allocated vested tokens worth 110% of their trading fees.
Example: with commissions currently configured to 0.1%, on a $1,000 notional position, a trader would have paid $2 total in fees [(0.001*1,000) + (0.001*1,000)] upon entrance of the trade and exit of the trade. At the end of the week, the trader could recoup $2.20 ($2 * 110%) in PERP tokens. Of this $2.20, 50% was available immediately, and 50% was available after a 6-month lockup period.
Staking Program
Example: $50,000 in total weekly commission fees are generated by the protocol. At current market price of $7.35, this would amount to 3,401.36 tokens [(0.5*50,000)/7.35]. Therefore, the remaining 146,598.64 tokens would come from the ecosystem and rewards fund. Suppose you made up 10% of the staking pool. You would receive 15,000 tokens at the end of the week. Of these tokens, 340.136 would be immediately liquid, while 14,659.865 would remain locked for 6 months.
Typically, staking tokens performs some value-add service to the network, whether that be securing and attesting to transactions (PoS), providing counterparty liquidity to trades (SNX) etc. While not as directly visible, PERP stakers are adding some functionality to the protocol. First, restricting token access (voluntarily or involuntarily) tends to lead to less available sell side liquidity which tends to push the price up. A strong PERP price is crucial to the network, as the system currently does not have an ADL feature (explained below). Similarly, capital restriction via a cool down period (14 days to unstake) prevents market supply from overreacting to volatility events that could result in the minting of new PERP tokens. Voluntarily surrendering liquidity incurs a set of native risks, and thus participants need to be compensated for such risk.
ADL/Insurance Fund
The Perpetual Protocol currently does not implement an auto-deleverage (ADL) feature. Each trader’s position has a defined liquidation point based on their margin ratio. If a trader’s position moves against them to the level where it breaches the liquidation point, the system will seize the position and unwind it, and take the underlying collateral. Traders also have a bankruptcy price, which is the max level in which the position can draw down against, without the trader’s account going into negative territory
Example:
Bob gets long 1 BTC at $50,000/BTC using $25,000 collateral (2x leverage)
Liquidation Price: $25,500/BTC
Bankruptcy Price: $25,000/BTC
If price collapses downwards and approaches $25,500 Bob, risks liquidation. If he gets liquidated the protocol will automatically close his position and confiscate his collateral. Suppose after slippage, the exchange unwinds Bob’s long position at a price of $25,400/BTC.
Closure Price: $25,400/BTC
Mathematically speaking, Bob’s collateral can support a price of up to $25,000 before he is fully wiped out. 25,400 - 25,000 = $400. So where does this money go?
What happens next varies from exchange to exchange. Bitmex would simply pocket the $400 and transfer it into the insurance fund. Other exchanges deposit a % of that $400 into the insurance fund, and return the remaining back to the trader. Or they will close a portion of the traders position (effectively realizing some PnL), as a way to deleverage them, and slow down their loss rate.
In the Perpetual Protocol, the keeper bots who initiate the transaction get to pocket 1.25% of the maintenance margin (recall that the lowest the maintenance margin can go before liquidation is 6.25%). The system will then attempt to perform partial liquidations as a way to keep the trader engaged in the position as long as possible.
Now, going back to our example, say that when the price crashes to $25,500/BTC the market goes into a no-bid death spiral. Liquidation occurs, but due to how thin the books are at the time, the system cannot unwind the position without incurring considerable slippage. Suppose the system can only execute that unwind at a price of $24,000/BTC
Closure Price: $24,000/BTC
24,000 - 25,000 = -1,000. Meaning the trader’s account would have a negative balance. But the system cannot force someone to deposit more funds to make good on a negative balance. So they have to account for this in an alternative manner.
This is what the insurance fund is utilized for. In the event that bad debt accrues on a trader’s position, the system will pull money from the insurance fund to make up the balance. It will keep doing this until the entire insurance balance is drained.
What happens if we eat through all the insurance fund capital, but bad debt still exists? Typically, ADL ensues. ADL is a process in which traders who are in profit, and not at any relative risk of getting liquidated, all of a sudden find themselves pushed out of their existing position, and their PnL realized. Think of it like you are playing high stakes tables at the casino and absolutely crushing it. All of a sudden a bouncer approaches you and demands that you cash out your chips and leave the venue, because you’re on the verge of bankrupting the house.
The culprit in our situation is lack of buy side demand. If there were ample long liquidity available in the market and a position entered liquidation, the closure price would be well in excess of the bankruptcy price, and everything would be fine. It's when that buy side demand dries up that problems ensue, because slippage on the execution could run it below bankruptcy.
By ADL’ing a profitable short, you are synthetically creating buy side demand, because in order to close a short, you have to perform the inverse function (go long). This creates an avenue where the protocol can find a buyer to sell the liquidated position into.
Perpetual does away with this ADL concept, and essentially utilizes PERP token holders as the backstop mechanism for bad debt. It does this by minting new tokens, selling them at market, and depositing the proceeds into the insurance fund to make even the bad debt. In this manner, the insurance fund is essentially infinite, so long as the price of PERP token remains above 0.
Oracle
The system requires an oracle module in order to calculate funding rates, and utilizes a chainlink BTC/USD feed comprised of 31 oracles. You can see full specs for the module here: https://data.chain.link/btc-usd
The mark price for a derivative is the price used to calculate liquidation. Typically, this mark price is calculated via a TWAP of the index oracle, rather than the TWAP of the derivative price. Due to the feature of leverage, if the derivative price was the underlying factor, the effects of cascading liquidations would lead to severe volatility in the derivative instrument that was not otherwise exhibited in the broader spot market, and expose the protocol to unnecessary manipulation risk.
Challenges
Insurance Fund Imbalances
Probably the most pressing issue that the protocol faces. With an orderbook model there’s harmony between aggregate short and long contracts outstanding. This allows trivial tethering to an underlying index, as there is an accountable counterparty the system can charge an interest rate to, in order to incentivize price back towards a specific direction. But this isn’t the case for a vAMM, since the system does not require an equal matching between long and short contracts. Suppose that there are only a few traders in the system, and all of them are long. Under these parameters, it is still possible that the BTC/USD PERP contract trades below the spot index price, and thus funding is negative (shorts paying longs). The dilemma here is that no shorts in which the system can levy an interest rate on. Thus, the protocol relies on the insurance fund to be that funding counterparty to the longs.
Over the last few months, funding on the PERP protocol has been consistently negative, despite its CEX competitors being positive, for the reasons described above. This has manifested itself with a slow drain on the insurance fund under periods of low volatility, which runs somewhat counter-intuitive to the norm. Interestingly, this dynamic creates an additional component of alpha for market neutral traders: they can short on a CEX where funding is positive, and collect the rate, then hedge their short exposure with a long on PERP where funding is negative, and collect another rate.
Another related challenge to the Insurance Fund is network latency of the Ethereum blockchain. During high volatility periods the blockchain tends to become congested. Because liquidations are triggered onchain by keeper bots, by the time the transaction is processed into an ETH block, the closure price of the trader’s position may fall below the bankruptcy price of said position, leaving the system in debt. The protocol cannot go after a trader and force them to deposit more collateral, so the difference is made up via the insurance fund pool.
Token Valuation
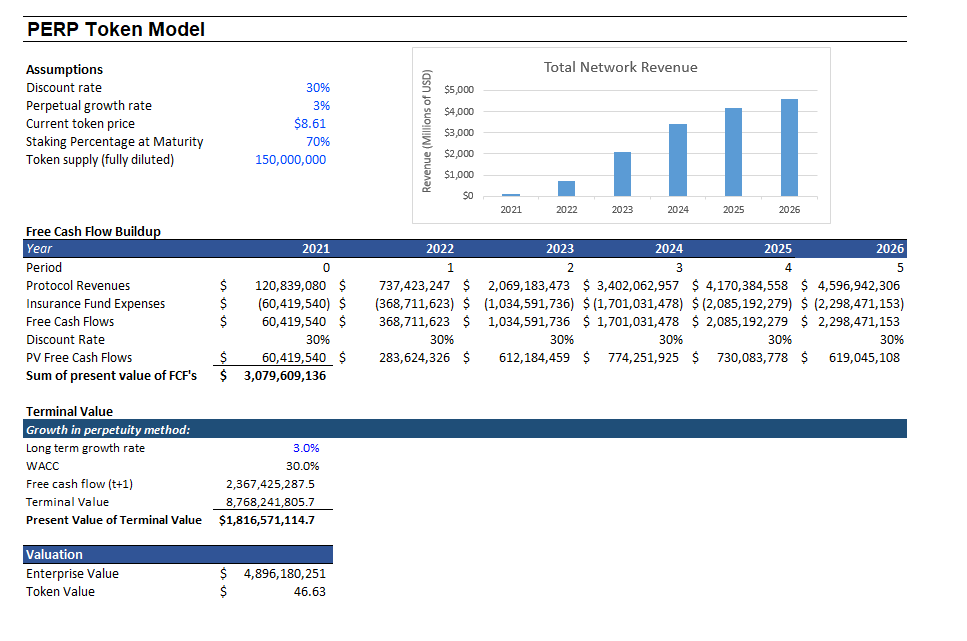
As the case with a growing number of DeFi cryptoassets, the PERP token generates cash flows that allow for valuation of PERP based on a Discounted Cash Flow analysis. PERP token price projections are modeled from both the early volume growth seen on the perpetual protocol as well as that from similar decentralized spot exchanges such as Uniswap and Sushiswap.
As outlined in the model below, assuming 70% of PERP tokens are staked at maturity (inline with percent staked in many L1 networks) and a total supply of 150 million tokens, the projected value of PERP is ~$47. Of note this is about a 500% increase from its current price of ~$8.
Summary
The Greymatter team is highly bullish on the concept of decentralized marketplaces for derivative instruments. With the demonstrated success of spot markets like Uniswap and Sushiswap, the explosion of volume in the centralized derivative landscape since 2017, and the impending regulatory crackdown of the prior, a decentralized alternative is in our minds, not a matter of if, but when. While the Perpetual Protocol indeed faces many architectural challenges, they are powered by a strong team with an all star lineup of backers. Derivative DEX’s are an extremely novel idea very much still in the proof of concept phase, so there is a tremendous amount of innovation and discovery to be made. Perpetual Protocol is positioned at the forefront of the industry, with a fully functional product boasting impressive growth rates.
Disclaimer
We do not endorse or recommend any investment action in the Perpetual Protocol token (PERP). This document should not be regarded as investment advice, offering document, or as a recommendation regarding a course of action.