Ring Signatures (Part 2): AOS Rings
In Part 1 of this series, I demonstrated how we convert the interactive Schnorr protocol into a non-interactive variant, using something…
In Part 1 of this series, I demonstrated how we convert the interactive Schnorr protocol into a non-interactive variant, using something called a Fiat-Shamir transformation. This sets the foundation for the Schnorr signature scheme.
AOS signatures, the first type of ring signature we will be discussing, builds heavily off of Schnorr.
The idea of AOS rings work as follows: Bob gathers public keys belonging to Alice, Carol and Dave from some directory. Because their keys are assumed to be public knowledge, the scheme requires no interaction from anyone outside of Bob. Alice, Carol and Dave may not even know that their keys are being used.
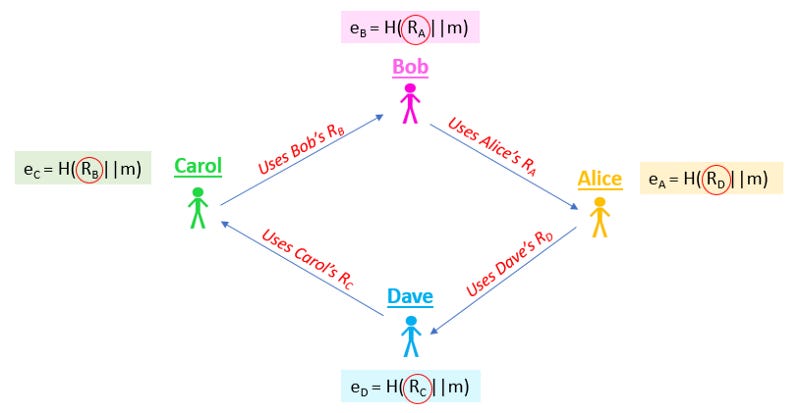
Bob then creates a Schnorr signature using his private key. Note that Bob does not have access to Alice, Carol or Dave’s private keys. Normally, this means that he would be incapable of issuing signatures on behalf of these individuals.
The AOS protocol flips this idea on its head. Using a bit of cryptographic magic, they allow a method for Bob to forge signatures on behalf of the external parties without knowing their private keys. These forged signatures are then concatenated with Bob’s valid signature to create a cohesive “group signature”.
Incredibly, if Bob’s portion of the group signature is produced legitimately (i.e. by using his private key), the forged portions representing Alice, Carol and Dave will appear equally legitimate from the perspective of a validator. Cryptographically speaking, the verifier can only decipher whether or not someone in the group signed their index using the private key. But they are incapable of determining which member it was.
This plausible deniability allows Bob to preserve his identity as the group’s coordinator, while at the same time, provide assurance to a validator that some member had knowledge of the private key, and was thereby authorized to create the ring.